回溯
77. 组合
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]示例 2:
输入:n = 1, k = 1 输出:[[1]]
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
vector<vector<int>> combine(int n, int k) {
dfs(n,k,1);
return result;
}
void dfs(int n,int k,int index) {
if(path.size() == k) {
result.push_back(path);
return;
}
for(int i = index; i <= n; i++) { //i<=(n-(k-path.size())+1)完成剪枝
path.push_back(i);
dfs(n,k,i+1);
path.pop_back();
}
}
};39. 组合总和
给你一个 无重复元素 的整数数组
candidates和一个目标整数target,找出candidates中可以使数字和为目标数target的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。对于给定的输入,保证和为
target的不同组合数少于150个。示例 1:
输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。示例 2:
输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]示例 3:
输入: candidates = [2], target = 1 输出: []提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
int sum;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
dfs(candidates,target,0);
return ans;
}
void dfs(vector<int>& candidates, int target,int index) {
if(sum > target) {
return;
}
if(sum == target) {
ans.push_back(path);
return;
}
// 如果 sum + candidates[i] > target 就终止遍历
for(int i = index;i < candidates.size()&&sum + candidates[i] <= target;i++) {
sum+=candidates[i];
path.push_back(candidates[i]);
dfs(candidates,target,i);
sum-=candidates[i];
path.pop_back();
}
}
};40. 组合总和 II
给定一个候选人编号的集合
candidates和一个目标数target,找出candidates中所有可以使数字和为target的组合。
candidates中的每个数字在每个组合中只能使用 一次 。**注意:**解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8, 输出: [ [1,1,6], [1,2,5], [1,7], [2,6] ]示例 2:
输入: candidates = [2,5,2,1,2], target = 5, 输出: [ [1,2,2], [5] ]提示:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
bool used = false;
dfs(candidates,target,0,used);
return ans;
}
void dfs(vector<int>& candidates, int target, int index,bool used) {
if(!target) {
ans.push_back(path);
return;
}
for(int i = index;i < candidates.size() && target > 0; i++) {
// used == true,说明同一树枝candidates[i - 1]使用过
// 要对同一树层使用过的元素进行跳过
if(i>0&&candidates[i]==candidates[i-1]&&!used) {
continue;
}
path.push_back(candidates[i]);
used = true;
dfs(candidates,target-candidates[i],i+1,used);
used = false;
path.pop_back();
}
}
};216. 组合总和 III
找出所有相加之和为
n的k个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。示例 2:
输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]] 解释: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 没有其他符合的组合了。示例 3:
输入: k = 4, n = 1 输出: [] 解释: 不存在有效的组合。 在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。提示:
2 <= k <= 91 <= n <= 60
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
int sum;
vector<vector<int>> combinationSum3(int k, int n) {
dfs(k,n,1);
return ans;
}
void dfs(int k, int n,int index) {
if(sum > n) { //剪枝
return;
}
if(path.size() == k && sum == n) {
ans.push_back(path);
return;
}
for(int i = index;i <= 9;i++) { //i <= 10-(k-path.size())可以剪枝
sum+=i;
path.push_back(i);
dfs(k,n,i+1);
sum-=i;
path.pop_back();
}
}
};257. 二叉树的所有路径
给你一个二叉树的根节点
root,按 任意顺序 ,返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。
示例 1:
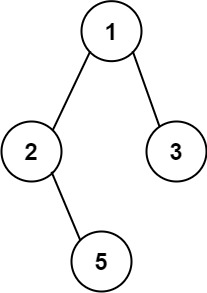
img 输入:root = [1,2,3,null,5] 输出:["1->2->5","1->3"]示例 2:
输入:root = [1] 输出:["1"]
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
if(root == NULL) return res;
dfs(root,"",res);
return res;
}
void dfs(TreeNode* root,string s,vector<string>& res) {
s += to_string(root->val);
if(root->left == nullptr && root->right == nullptr) {
res.push_back(s);
return;
}
if(root->left) dfs(root->left, s + "->", res);
if(root->right) dfs(root->right, s + "->", res);
}
};17. 电话号码的字母组合
给定一个仅包含数字
2-9的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
img 示例 1:
输入:digits = "23" 输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]示例 2:
输入:digits = "" 输出:[]示例 3:
输入:digits = "2" 输出:["a","b","c"]
class Solution {
public:
vector<string> ans;
string path;
unordered_map<char, string> phoneMap{
{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}
};
vector<string> letterCombinations(string digits) {
if(digits.size() == 0) {
return ans;
}
dfs(digits,0);
return ans;
}
void dfs(string digits,int index) {
if(path.size() == digits.size()) {
ans.push_back(path);
return;
}
char digit = digits[index];
string s = phoneMap.find(digit)->second;
for(int i = 0;i < s.size();i++) {
path.push_back(s[i]);
dfs(digits,index+1);
path.pop_back();
}
}
};131. 分割回文串
给你一个字符串
s,请你将s分割成一些子串,使每个子串都是回文串
返回
s所有可能的分割方案。示例 1:
输入:s = "aab" 输出:[["a","a","b"],["aa","b"]]示例 2:
输入:s = "a" 输出:[["a"]]提示:
1 <= s.length <= 16s仅由小写英文字母组成
class Solution {
public:
vector<vector<string>> ans;
vector<string> path;
vector<vector<string>> partition(string s) {
dfs(s,0);
return ans;
}
//判断s[i, j]是否为回文串
bool isPalindrome(string s,int i,int j) {
while(i<=j) {
if(s[i++] != s[j--]) {
return false;
}
}
return true;
}
void dfs(string s,int index) {
if(index == s.size()) {
ans.push_back(path);
return;
}
for(int i = index;i < s.size();i++){
if(isPalindrome(s,index,i)){
path.push_back(s.substr(index,i-index+1));
dfs(s,i+1);
path.pop_back();
}
}
}
};93. 复原 IP 地址
有效 IP 地址 正好由四个整数(每个整数位于
0到255之间组成,且不能含有前导0),整数之间用'.'分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 无效 IP 地址。给定一个只包含数字的字符串
s,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在s中插入'.'来形成。你 不能 重新排序或删除s中的任何数字。你可以按 任何 顺序返回答案。示例 1:
输入:s = "25525511135" 输出:["255.255.11.135","255.255.111.35"]示例 2:
输入:s = "0000" 输出:["0.0.0.0"]示例 3:
输入:s = "101023" 输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]提示:
1 <= s.length <= 20s仅由数字组成
class Solution {
public:
vector<string> res;
void backTracking(string& s, int startIndex, int pointNum) {
if(pointNum == 3) {
if(isValid(s, startIndex, s.size() - 1)) {
res.push_back(s);
}
return;
}
for(int i = startIndex; i < s.size(); i++) {
if(isValid(s, startIndex, i)) {
s.insert(s.begin() + i + 1, '.');
pointNum++;
backTracking(s, i+2, pointNum);
pointNum--;
s.erase(s.begin() + i + 1);
}
}
}
bool isValid(const string& s, int start, int end) {
if(start > end) {
return false;
}
if(s[start] == '0' && start != end) {
return false;
}
int num = 0;
for(int i = start; i <= end; i++) {
if(s[i] > '9' || s[i] < '0') {
return false;
}
num = num * 10 + (s[i] - '0');
if(num > 255) {
return false;
}
}
return true;
}
vector<string> restoreIpAddresses(string s) {
if(s.size() > 12) {
return res;
}
backTracking(s, 0, 0);
return res;
}
};78. 子集
给你一个整数数组
nums,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3] 输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]示例 2:
输入:nums = [0] 输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> subsets(vector<int>& nums) {
dfs(nums,0);
return ans;
}
void dfs(vector<int>& nums,int index) {
ans.push_back(path);
for(int i = index; i < nums.size();i++) {
path.push_back(nums[i]);
dfs(nums,i+1);
path.pop_back();
}
}
};90. 子集 II
给你一个整数数组
nums,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2] 输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]示例 2:
输入:nums = [0] 输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10
class Solution {
public:
vector<vector<int>> ans;;
vector<int> path;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(),nums.end());
vector<bool> used(nums.size());
dfs(nums,used,0);
return ans;
}
void dfs(vector<int>& nums,vector<bool>& used,int index) {
ans.push_back(path);
for(int i = index; i < nums.size(); i++) {
if(i>=1&&nums[i] == nums[i-1]&&!used[i-1]) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
dfs(nums,used,i+1);
path.pop_back();
used[i] = false;
}
}
};491. 非递减子序列
给你一个整数数组
nums,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。示例 1:
输入:nums = [4,6,7,7] 输出:[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]示例 2:
输入:nums = [4,4,3,2,1] 输出:[[4,4]]提示:
1 <= nums.length <= 15-100 <= nums[i] <= 100
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> findSubsequences(vector<int>& nums) {
dfs(nums,0);
return ans;
}
void dfs(vector<int>& nums,int index) {
if(path.size()>=2){
ans.push_back(path);
}
unordered_set<int> set;
for(int i = index; i < nums.size(); i++) {
if(path.size() > 0 && nums[i] < path.back() || set.find(nums[i]) != set.end()) {
continue;
}
set.insert(nums[i]);
path.push_back(nums[i]);
dfs(nums,i+1);
path.pop_back();
}
}
};46. 全排列
给定一个不含重复数字的数组
nums,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。示例 1:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2:
输入:nums = [0,1] 输出:[[0,1],[1,0]]示例 3:
输入:nums = [1] 输出:[[1]]提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> used(nums.size());
dfs(nums,used);
return ans;
}
void dfs(vector<int>& nums,vector<bool>& used) {
if(path.size() == nums.size()){
ans.push_back(path);
return;
}
for(int i = 0; i < nums.size(); i++) {
if(used[i]) {
continue;
}
used[i] = true;
path.push_back(nums[i]);
dfs(nums,used);
used[i] = false;
path.pop_back();
}
}
};47. 全排列 II
给定一个可包含重复数字的序列
nums,按任意顺序 返回所有不重复的全排列。示例 1:
输入:nums = [1,1,2] 输出: [[1,1,2], [1,2,1], [2,1,1]]示例 2:
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]提示:
1 <= nums.length <= 8-10 <= nums[i] <= 10
class Solution {
public:
vector<vector<int>> ans;
vector<int> path;
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(),nums.end());
vector<bool> used(nums.size());
dfs(nums,used);
return ans;
}
void dfs(vector<int>& nums,vector<bool>& used) {
if(path.size() == nums.size()) {
ans.push_back(path);
return;
}
for(int i = 0; i < nums.size();i++) {
if(i>0&&nums[i]==nums[i-1]&&!used[i-1]||used[i]) {
continue;
}
used[i] = true;
path.push_back(nums[i]);
dfs(nums,used);
used[i] = false;
path.pop_back();
}
}
};51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中
'Q'和'.'分别代表了皇后和空位。示例 1:
img 输入:n = 4 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释:如上图所示,4 皇后问题存在两个不同的解法。示例 2:
输入:n = 1 输出:[["Q"]]提示:
1 <= n <= 9
class Solution {
public:
vector<vector<string>> ress;
bool isValid(vector<string>& res, int row, int col, int n) {
for (int i = row; i >= 0; i--) {
if (res[i][col] == 'Q'){
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (res[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (res[i][j] == 'Q') {
return false;
}
}
return true;
}
void backtracing(int& n, vector<string>& res, int row) {
if (row == n) {
ress.push_back(res);
return;
};
for (int col = 0; col < n; col++) {
if (!isValid(res, row, col, n))
continue;
res[row][col] = 'Q';
backtracing(n, res, row + 1);
res[row][col] = '.';
}
}
vector<vector<string>> solveNQueens(int n) {
vector<string> res(n, string(n, '.'));
backtracing(n, res, 0);
return ress;
}
};37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。- 数字
1-9在每一列只能出现一次。- 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)数独部分空格内已填入了数字,空白格用
'.'表示。示例 1:
img 输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释:输入的数独如上图所示,唯一有效的解决方案如下所示:提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
class Solution {
private:
bool dfs(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] == '.') {
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (dfs(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
dfs(board);
}
};